[자료구조] 트리, 이진트리
트리란?
1개 이상의 노드를 갖는 집합. 하나의 노드를 중심으로 나머지 노드들이 뻗어나가는 구조다.

트리의 필요성
- 트리는 빠른 탐색에 강점을 보인다. 연결리스트는 특정 노드로 찾아가려면 노드의 처음부터 탐색해야 해서 시간이 꽤 걸리는데, 트리가 이 문제를 보완해준다.
- 노드 간의 순서가 있거나 노드들이 포함관계일 때 트리는 그 관계를 통해 노드를 찾을 수 있다.
트리 용어

노드 : 한 정보 아이템 + 다른 노드로 뻗어진 가지
부모(<-> 자식) : 부속 트리를 가진 노드 (ex E의 부모는 B)
형제 : 같은 부모를 가진 노드 (ex E의 형제는 F)
루트 : 최상위에 있는 노드 (ex 루트는 A)
노드의 차수 : 특정 노드의 자식 수 (ex B의 차수는 2)
트리의 차수 : max(노드의 차수) (ex 3)
단말(리프) 노드 : 차수가 0인 노드, 최하위에 있는 노드 (ex 단말 노드는 K,L,F,G,M,I,J)
비단말 노드 : 차수가 0이 아닌 노드, 단말 노드가 아닌 노드
레벨 : 루트 레벨==1, 자식 레벨==부모 레벨+1
높이(깊이) : max(레벨)
이진 트리
트리를 효과적으로 활용하기 위해서는 일반트리보다 이진트리를 사용하는것이 좋다.
이진트리란, 각 노드가 최대 2개의 자식을 갖는 트리를 말한다.

일반 트리와 이진 트리의 차이점
- 각 노드는 항상 두개 이하의 자식을 가져야 한다
- 왼쪽 자식노드와 오른쪽 자식노드가 구별된다
- 노드가 없는 공백 이진 트리가 존재한다.

이진트리의 성질
i 레벨의 최대 노드 수 : 2^(i-1)
깊이가 k인 트리의 최대 노드 수 : 2^(k)-1
(n = 총 노드 수, n0 = 리프 노드 수, n1 = 차수가 1인 노드 수, n2 = 차수가 2인 노드 수, B = 총 가지의 수)
차수가 1인 노드 수 (n1) = n2 + 1
총 노드 수(n) = n0 + n1 + n2
= B + 1 (루트를 제외한 모든 노드들은 부모에게서 온 가지가 하나씩 있으므로)
총 가지의 수(B) = n1 + 2*(n2) (모든 가지들은 차수가 2 or 1인 노드에서 뻗어나오므로)
리프 노드 수(n0) = n2 + 1 (위 식을 조합하여)
이진 트리 종류
- 편향 이진 트리 : 왼쪽이나 오른쪽 자식만을 갖고 있는 트리
- 완전 이진 트리 : - 마지막 레벨을 제외하고 모든 레벨이 꽉 채워져있는 트리
- n개의 노드를 갖는 트리의 높이 = log2(n+1) 의 소수점 올림한 값
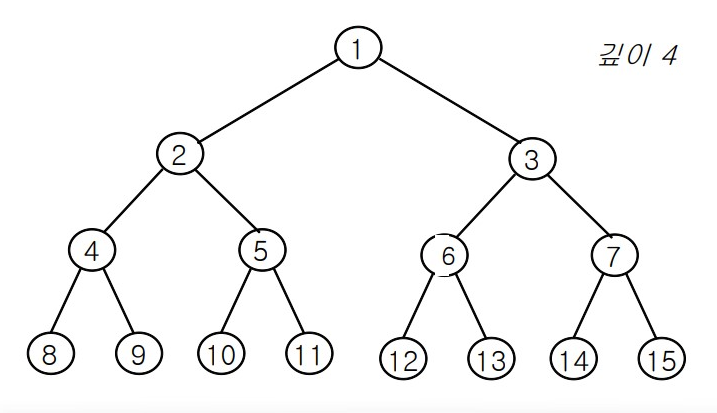
- 포화 이진 트리 : 모든 레벨이 꽉 채워져 있는 트리

참고 자료:
C++ 자료구조론/이석호 역/인피니티북스/2007/2판