[자료구조] 이진 트리 구현, 트리 순회 구현
일반 트리에서 이진 트리로 변환하는 법
왼쪽 자식-오른쪽 형제 표현을 활용한다
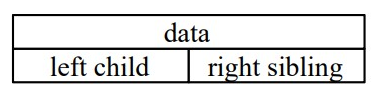
일반트리를 이진트리로 변환하려면 한 노드당 가진 자식을 2개 이하로 줄여야 한다. 그러기 위해 왼쪽 자식-오른쪽 형제 표현을 활용한다. 이 표현은 위 그림과 같이 각 노드에 값(data), 왼쪽자식의 주소(left child), 오른쪽 형제의 주소(right sibling)를 담는 방법이다. 노드 클래스를 만들 때 이 세 멤버변수를 넣는다. 표현을 적용 하면 아래 그림과 같이 트리가 그려지고, 그 트리를 45도로 회전시키면 이진트리 모양으로 바뀐다. 이로써 일반트리가 노드당 두개의 자식만 가지게 되었다. 하지만 해당 트리를 활용할 때 실제로 오른쪽 노드는 자식이 아닌 형제관계임을 인지해야 한다.
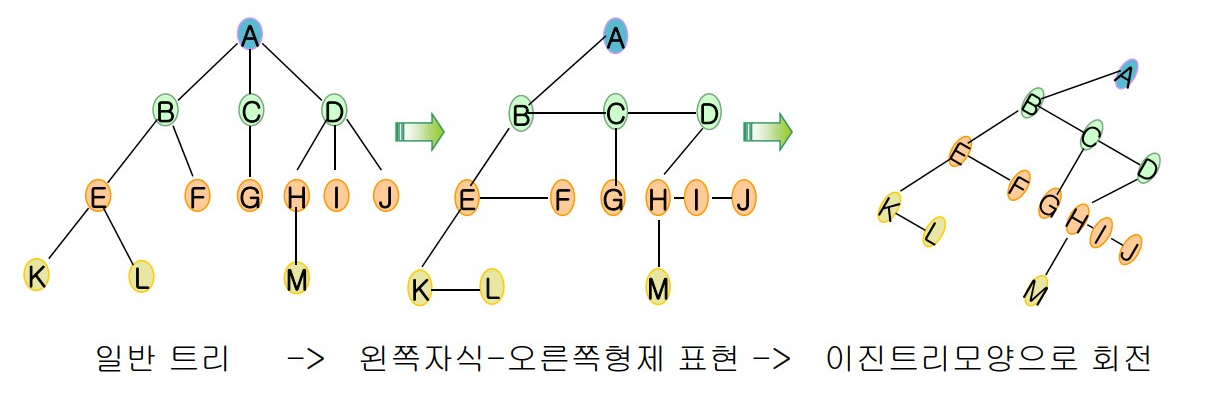
이진 트리 노드 구현
이진 트리의 각 노드에는 값(data), 왼쪽 자식의 주소(leftChild), 오른쪽 자식의 주소(rightChild)를 담고 있어야 한다.

노드 클래스
class TreeNode{
public:
TreeNode(int mydata){
data = mydata;
leftChild = 0;
rightChild = 0;
}
private:
int data;
TreeNode *leftChild;
TreeNode *rightChild;
}
모든 노드를 한번씩 방문하기 (트리 순회)
트리를 순회하는 방법은 대표적으로 4가지가 있다. 4가지 방법 모두 루트 노드에서 시작한다.
중위 순회 (LVR(left visit right)) : 왼쪽 자식부터 방문 후 오른쪽 자식 방문하는 방법
왼쪽 자식으로 끝없이 이동, 왼쪽 자식이 없으면 방문, 이후 오른쪽 자식으로 한번 이동, 그리고 다시 왼쪽자식으로 끝없이 이동...반복
전위 순회 (VLR(visit left right)) : 루트 노드부터 방문하는 방법
새로운 노드로 이동하면 바로 방문. 이동 순서는 왼쪽 자식 먼저, 왼쪽 자식 없으면 오른쪽 자식.
후위 순회 (LRV(left right visit)) : 리프 노드부터 방문하는 방법
왼쪽 자식으로 끝없이 이동, 왼쪽 자식이 없으면 오른쪽 자식으로 한번 이동, 그리고 다시 왼쪽자식으로 끝없이 이동, 왼쪽 자식이 없으면 오른쪽 자식으로 한번 이동, 오른쪽 자식도 없으면 방문
층별 순회 : 위에서 아래로 방문하는 방법
루트부터 레벨 순서대로 방문

위 그림의 이진트리(오른쪽 트리)를 순회한 결과
중위 순회(LVR) : K -> L -> E -> F -> B -> G -> C -> M -> H -> J -> I -> D -> A
전위 순회(VLR) : A -> B -> E -> K -> L -> F -> C -> G -> D -> H -> M -> I -> J
후위 순회(LRV) : L -> K -> F -> E -> G -> M -> J -> I -> H -> D -> C -> B -> A
레벨 순회 : A -> B -> E -> C -> K -> F -> G -> D -> L -> H -> M -> I -> J
트리 순회 구현
- 재귀 호출을 사용하여 구현한다.
- Visit() 함수 : 노드를 방문하는 함수
중위 순회 구현 코드
void Inorder(TreeNode* CurrentNode){
if(CurrentNode) {
Inorder(CurrentNode->leftchild);
Visit(CurrentNode);
Inorder(CurrentNode->rightChild);
}
}
전위 순회 구현 코드
void Preorder(TreeNode* CurrentNode){
if(CurrentNode){
Visit(CurrentNode);
Inorder(CurrentNode->leftchild);
Inorder(CurrentNOde->rightChild);
}
}
후위 순회 구현 코드
void Postorder(TreeNode* CurrentNode){
if(CurrentNode){
Postorder(CurrentNode->rightChild);
Postorder(CurrentNode->leftchild);
Visit(CurrentNode);
}
}
레벨 순회 구현
- 큐를 활용한다.
- 동작 과정
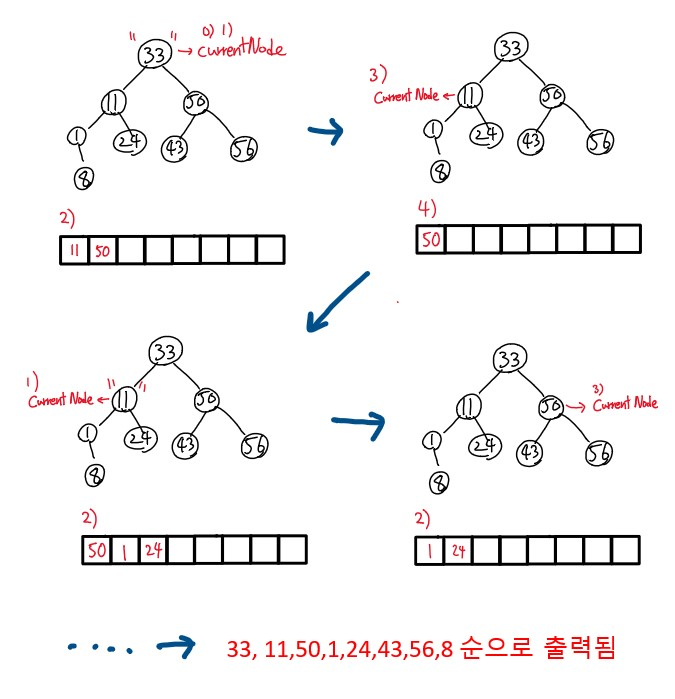
0) 현 노드(currentNode)를 root로 지정.
1) 현 노드 출력
2) 현 노드의 왼쪽 자식과 오른쪽 자식을 큐에 삽입
3) 가장 먼저 큐에 삽입된 값을 호출(q.front())하여 현 노드로 설정
4) 가장 먼저 큐에 삽입된 값 삭제 (q.pop())
1~4 반복
레벨 순회 구현 코드
#include <queue>
void LevelOrder(TreeNode* root){
queue <TreeNode*> q;
TreeNode* currentNode = root; // 0)
while(currentNode){
Visit(currentNode); // 1)
if(currentNode->leftChild) q.push(currentNode->leftChild); // 2)
if(currentNode->rightChild) q.push(currentNode->rightChild); // 2)
if(q.empty()) return;
currentNode = q.front(); // 3)
q.pop(); // 4)
}
}